Graph theory play very important role when we deal with network information (such as social network, biomedical network, web & citations, internet analysis etc). Graph theory has different types of applications within Data Science. Graph theory is fundamental to the development of many algorithms used in Google page rank or Netflix content recommendation. Let's understand the basics of the graph theory.
- The number of edges incident on a vertex vi, with self loop counted twice, is called degree, d(vi), of the vertex vi.
- In Fig 1, d(v1)=d(v3)=d(v4)=3, d(v2)=4 and d(v5)=1.
- The sum of the degrees of all vertices in a graph with e edges and n vertices is twice the number of edges.
- In Fig 1, d(v1)+d(v3)+d(v4)+d(v2)+ d(v5)=3 + 4 + 3 + 3 + 1
= 14 = Twice the number of edges.
- The number of vertices of odd degree in graph is always even.
Walks
- A walk is defined as a finite alternating sequence of vertices and edges, beginning and ending with vertices, such that each edge is incident with the vertices preceding and following it.
- No edge appears more than once in a walk.
- However a vertex may appear more than once.
Example: Walk
 |
| Fig 2: graph |
- In the above graph v1 a v2 b v3 c v3 d v4 e v2 f v5 is a walk.
- Vertices with which a walk begins and ends are called its terminal vertices.
Closed and open walk
- If a walk begins and ends with same vertex then then it is called closed walk (terminal vertices are same).
- If a walk begins and ends with distinct vertices then it is called open walk (distinct terminal vertices).
- In previous slide, the walk given is open walk.
Path
- An open walk in which no vertex appears more than more than once is called a path.
- In Fig 2, v1 a v2 b v3 d v4 is a path whereas v1 a v2 b v3 c v3 d v4 e v2 f v5 is not a path.
- Number of edges in a path is called the length of a path.
- A self loop can be included in a walk but not in a path.
Circuit
- A closed walk in which no vertex (except the initial and final vertex) appears more than once is called a circuit.
- A circuit is a closed, non-intersecting walk.
- In Fig 2, v2 b v3 d v4 e v2 is a circuit.
- A circuit is also called a cycle, elementary cycle, circular path, and polygon.
Subgraph
A graph g is said to be a sub graph of a graph G if all the vertices and all the edges of g are in G, and each edges of g has the same end vertices in g as in G.
The concept of graph is akin to the concept of subset in set theory.
The symbol of subset from set theory is used in stating “g is a sub graph of G.
 |
| Fig 3: Graph and Subgraph |
Graph in Fig 3(b) is a subgraph of the one in Fig 3(a).
Subgraph Observations
Every graph is its own subgraph.
A subgraph of a subgraph of G is a subgraph of G.
A single vertex in a graph G is a sungraph of G.
A single edge in G, together with end vertices, is also a subgraph of G.
Edge-Disjoint Subgraph
Two (or more) subgraphs g1 and g2 of a graph G are said to be edge disjoint if g1 and g2 do not have any edges in common.
Connected Graphs
A graph is connected if we can reach any vertex from any vertex by traveling along the edges.
A graph G is said to be connected if there is at least one path between every pair of vertices in G.
Otherwise the graph is disconnected.
A disconnected graph consists of two or more connected graphs. These connected subgraphs are called Component.
Theorems on Connected graphs
- A graph G is disconnected iff its vertex set V can be partitioned into two nonempty, disjoint subsets V1 and V2 such that there exists no edge in G whose one end vertex is in subset V1 and the other in subset V2.
- If a graph (connected or disconnected) has exactly two vertices of odd degree, there must be a path joining these two vertices.
- A simple graph (without parallel or self-loop) with n vertices and k components can have at most (nk)(n-k+1)/2 edges.
Euler Graphs
If some closed walk in a graph contains all the edges of the graph, then the walk is called an Euler Line and the graph is called an Euler Graph.
Euler graph is always connected, except for any isolated vertices the graph may have.
Theorem: A given connected graph G is an Euler graph if and only if all vertices of G are of even degree.
A connected graph is unicursal if and only if it has exactly two vertices of odd degree.
A connected graph G is an Euler graph if and only if it can be decomposed into circuits.
An Euler graph G is arbitrarily traceable from vertex v in G if and only if every circuit in G contains v.
Example: Euler Graph
 |
| Fig 4: Example 1- Euler Graph |
 |
| Fig 5: Example 2 - Euler Graph |
Example : Unicursal Graph
 |
| Fig 6: Unicursal Graph |
Operations on graph
Union
The union of two graphs G1 = (V1, E1) and G2 = (V2, E2) is another graph G3 (written as G3 = G1UG2) whose vertex set V3 = V1 U V2 and the edge set E3 = E1 U E2.
Intersection
The intersection of two graphs G1 = (V1, E1) and G2 = (V2, E2) is another graph G3 (written as G3 = G1 ⋂ G2) whose vertex set V3 = V1 ⋂ V2 and the edge set E3 = E1 ⋂ E2.
Ring sum
The ring sum of two graphs G1 and G2 is a graph consisting of the vertex set V1 U V2 and of edges that either in G1 or G2 but not in both.
Deletion
If vi is a vertex in a graph G, then G-vi denotes a subgraph of G obtained by deleting vi from G. Deletion of a vertex always implies the deletion of all edges incident on that vertex.
Example: Graph Operations
 |
| Fig 7: Graph Operations |
Example: Deletion
 |
| Fig 8: Deletion in Graph - vertex and edge deletion |
Fusion
A pair of vertices a, b in a graph are said to be fused (merged or indentified) if the two vertices are replaced by a single new vertex such that every edge that was incident on either a or b or on both is incident on the new vertex.
Fusion of two vertices does not alter the number of edges, but it reduces the number of vertices by one.
Example: Fusion
 |
| Fig 9: Fusion of vertices |
Isomorphism
Two graphs G and G’ are said to be isomorphic to each other if there is a one-to-one correspondence between their vertices and between their edges such that the incidence relation is preserved.
In other words suppose that edge e is incident on vertices v1 and v2 in G; then the corresponding edge e’ in G’ must be incident on the vertices v’1 and v’2 that correspond to v1 and v2 respectively.
Example: Isomorphism
 |
| Fig 10 (a) |
 |
| Fig 10 (b) |
- Above two graphs are isomorphic.
- Vertices a, b, c, d, and e correspond to v1, v2, v3, v4 and v5 respectively. The edges 1, 2, 3, 4 5 and 6 correspond to e1, e2, e3, e4, e5 and e6 respectively.
Examples
 |
| Fig 11: Isomorphic Graphs |
Hamiltonian Circuit and Path
A Hamiltonian circuit in a connected graph G is defined as a closed walk that traverse every vertex of G exactly once, except of course the starting vertex.
A circuit in a connected graph G is said to be Hamiltonian if it includes every vertex of G.
If we remove any one edge from a Hamiltonian circuit, we left with a path. This path is called Hamiltonian path.
Example: Hamiltonian circuit
 |
| Fig 12: Hamiltonian Circuits |
Complete Graph
A simple graph in which there exists an edge between every pair of vertices is called a complete graph.
 |
| Fig 13: Complete Graphs |
- Complete graph are also known as universal graph and clique.
- Total number of edges in complete graph is n(n-1)/2.
- Total number of edge disjoint Hamiltonian circuits in a complete graph are (n-1)/2.
- Hamiltonian circuit possible without edge disjoint (n-1)!.
Tree
A tree is a connected graph without any circuit.
 |
| Fig 14: Tree |
Properties of TREES
- There is one and only one path between every pair of vertices in a tree.
- If in a graph G there is one and only one path between every pair of vertices, G is a tree.
- A tree with n vertices has n-1 edges.
- Any connected graph with n vertices and n-1 edges is a tree.
- A graph is a tree if and only if it is minimally connected.
- A graph G with n vertices, n-1 edges, and no circuit is connected.
Pendant vertices in a tree
A pendant vertex is defined as a vertex of degree one.
In any tree (with two or more vertices), there are at least two pendant vertices.
Distance in a tree
• In a connected graph G, the distance d(vi, vj) between two vertices vi and vj is the shortest path (i.e. the number of edges in the shortest path) between them.
• A function that satisfies the three conditions i.e. non negativity, symmetry and triangle inequality is called a metric.
• The distance between vertices of a connected graph is a metric.
 |
| Fig 15: Distance in a tree |
• There are many paths between the vertices v1 and v2 but paths (a, e) and (a, f) are shortest of length 2. hence d(v1, v2)=2.
Eccentricity and center
• The eccentricity E(v) of a vertex v in a graph G is the distance from v to the vertex farthest from v in G; that is• A vertex with minimum eccentricity in graph G is called a center of G.
 |
| Fig 16: Tree |
• In above figure E(a)=2, E(b) = 1, E(c) = 2 and E(d) = 2.
• Hence vertex b is the center of the that tree.
 |
| Fig 17: Eccentricities of the vertices in a tree |
• Every tree has either one or two centers.
Binary Trees
• A binary tree is defined as a tree in which there is exactly one vertex of degree two and each of the remaining vertices is of degree one or three. |
| Fig 18: Binary Tree Graph |
Spanning Trees
• A tree T is said to be a spanning tree of a connected graph G if T is a subgraph of G and T contains all vertices of G.
• A given graph has numerous subgraphs from e edges, 2^e distinct combinations are possible.
• A spanning tree is a maximal tree subgraph or maximal tree of G.
 |
| Fig 19: Spanning Tree |
• In the below graph, the subgraph in heavy lines is a spanning tree of the graph shown.




















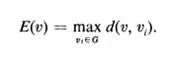
Comments
Post a Comment